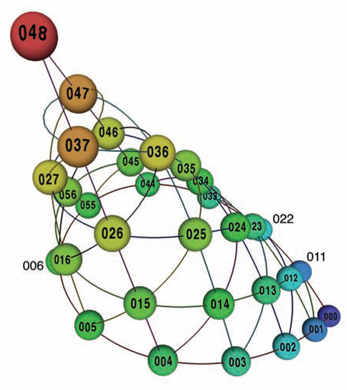
refer to pitch classes, with 0 = C, 1 = C#, etc. Points
represent equivalence classes of transpositionally related
chords. Thus, (C, D, E) and (D, E, F#) are both instances of
024. (Image made with Dmitri Tymoczko's
"ChordGeometries" program available here.)
Through the ages, the sound of music in myriad incarnations has captivated human beings and made them sing along, and as scholars have suspected for centuries, the mysterious force that shapes the melodies that catch the ear and lead the voice is none other than math.
It’s geometry, to be more precise, and now, a trio of 21st-century music professors from Florida State University, Yale University and Princeton University have analyzed and categorized in brand-new ways the mathematics intrinsic to musical harmony. Their cutting-edge collaboration has produced a powerful tool they call “geometrical music theory,” which translates the language of music theory into that of contemporary geometry.
The research is described in the April 18 issue of the journal Science, where the publication of work by music theorists and composers is rare if not unprecedented, said Clifton Callender, an assistant professor of composition in FSU’s College of Music. Callender is co-author of the paper “Generalized Voice-Leading Spaces” with Ian Quinn of Yale and Dmitri Tymoczko of Princeton.
“Our research offers a variety of tools for understanding and exploring music by drawing upon contemporary mathematics in natural and musically relevant ways,” Callender said. “It also provides a way to compare chords, and represents all possible combinations of pitches, including those found in non-Western music and avant-garde works that don’t conform to the traditional scales of Western music.”

As a result, composers could explore all sorts of uncharted musical possibilities; musicians may well be trained differently; new types of toys and musical instruments might be created; and music could be manifested visually (and geometry manifested aurally) in previously unimagined ways.
Geometrical music theory represents a culminating moment in the longstanding marriage of music and math. That marriage began when Pythagoras described pleasing musical intervals with simple mathematical ratios more than 2,600 years ago and further evolved during the Middle Ages when deep thinkers used those same ratios to model the “music of the spheres”—what many at that time believed to be the literally harmonious movements of the sun, moon and planets.
Understanding and interpreting music, say the authors of the study, is a process of discarding information—which in turn is the key to discovering its underlying mathematical structure.
A chord, for example, may be variously described as “the opening chord of Bach’s G minor Sonata for Unaccompanied Violin,” “G minor triad,” “minor triad” or simply “triad.”
“Each of these terms can refer to the same musical object at different levels of abstraction,” Callender said.
“We also experience a sense of distance when moving from one chord to another,” he said. “Changing one note just a little feels like a small motion between similar chords, while changing many notes by large amounts feels like a large motion between dissimilar chords.
“So, building on my own research and that of my Princeton colleague, our research modeled these spatial intuitions about chords at various levels of abstraction geometrically, using what mathematicians call ‘quotient spaces.’ Most of those spaces are warped and twisted such that they contain multiple ‘straight’ paths connecting any pair of points,” Callender said.
“Imagine being near the peak of a mountain and needing to get to the immediately opposite location,” he said. “You could proceed clockwise around the peak, counter-clockwise, or directly over the peak. These same three paths represent unique types of motions between major and minor triads in the space of three-note chord types, which is a cone. In fact, these motions and chords have been ubiquitous in Western music since medieval times to the present day.”
At each level of abstraction, musical objects are grouped into families of chords or melodies. Mathematical structure is assigned to the “families” so that they can be represented as points within complex geometrical spaces in much the same way that “x” and “y” coordinates correspond to points on a two-dimensional plane in simple high school algebra. The different families produce an exotic maze of diverse geometrical spaces such as twisted triangular donuts and pinched cones—and even some spaces that mathematicians haven’t dreamed up names for yet.
“My fellow researchers and I have found it thrilling to discover unexplored areas of mathematics in the course of solving musical problems,” Callender said.
“Professor Callender and his colleagues at Yale and Princeton are working at the forefront in this rarified area of music theory,” said Don Gibson, dean of the FSU College of Music. “Their research—and its publication in Science—represents a signal achievement in the discipline.”




